| Home | Ray Traced models | Anaglyphs | Interactive models | Virtual Flowers | About me | Tunes | Jacob Van Eyck | Fractal Tune Smithy |

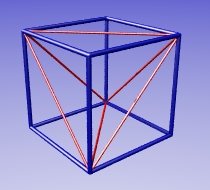
As this picture shows, the regular tetrahedron of side root two is obtained from the cube of side one by removing four right-angled tetrahedra of height one and base area half, which gives a volume one sixth each.
The octahedron of side one consists of two square pyramids each of height one over root two (half of root two) and base area one, so that's easy.
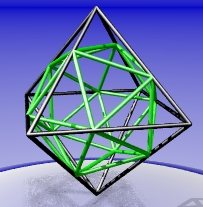
You can find the volume of the icosahedron by subtracting the volumes of twelve identical small irregular tetrahedra from the volume of the octahedron (two at each vertex). You can use the fact that its vertices meet the edges of the octahedron in the golden ratio to find the height and area of the base of the tetrahedron.
You can also calculate the lengths of the sides of the smaller icosahedron, and so confirm for yourself that this way of constructing an icosahedron from an octahedron does work - the edges are all the same length.

To obtain the volume of the dodecahedron, find the volume of the "tent" shape that you need to add to the six sides of the cube, which you can find in a few steps, using the fact that the ratio of a diagonal of a pentagon to its side is the golden ratio.
This image shows the dodecahedron, tetrahedron and octahedron.

Notice that the red tetrahedron can be obtained from the black octahedron by adding half size tetrahedra to four of its eight faces.
More mathematical images (start of page)
More mathematical images (volumes)