You probably have noticed the icon for Tune Smithy which looks like a red snowflake. It is actually based on a well known visual fractal called the Koch snowflake.
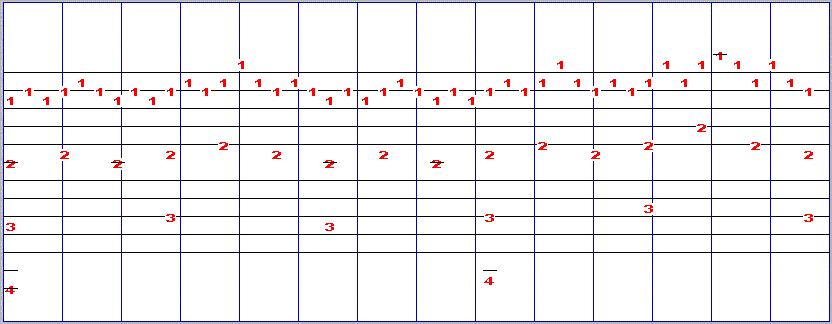
Here are the notes for the String Quintet - with 1s for layer 1, 2s for layer 2 and so on:

Here is the Koch snowflake - if you wait then it will go through the various stages of construction to more and more intricate detail

And here is an animation to show how the tune can be built up from the original phrase using passing tones one at a time.

(treble clef, pentatonic scale, scale of A, sharps in dark blue)
Two steps after the last frame in the animation, as a graph. This time in the whole tone scale, to give equal spacings in pitch between the notes.
The fractal melodies are like the Koch snowflake, but you build them up outwards rather than inwards, because it works more easily that way in music.
You can't go inwards to smaller and smaller details so easily in music because there are minimum pitch intervals between notes in the usual types of scale. However it can be done with unusual scales.
One way of going inwards to smaller pitch intervals
One can make scales with indefinitely small intervals, in an attempt at a closer parallel to the geometric case, and they can be interesting.
Try a scale with steps of an octave, then a third of an octave, then a ninth of an octave, and so on, or in cents:
0 cents 1200 cents 1600 cents 1733.333333 cents 1777.777777 cents 1792.592592 cents, ... (approaching 1800 cents and never quite reaching it).
The seed is 0 1 0 as before.
As you add extra notes between each one shown, the space beneath the curve remains clear, apart from some notes very close to the ones shown. The space above the curve shown eventually fills up with lines, as between any pair of notes you can find another one as close as you like to 1800 cents - one and a half octaves above the first note of the scale. It's not a continuous curve, but it has a type of exact self similarity. Can you see that the whole pattern is echoed in it's centre third? Also each third is echoed in its centre third? Can you see how the echoes continue to smaller and smaller copies?
The self similarity is of the same general type of pattern as the Koch snowflake, fractals with exact self similarity. The method of construction is similar too, adding identical smaller copies of a pattern to each of it's components. One could perhaps more exactly call this fractal the musical equivalent of Cantor's dust (Maths Encyclopedia entry).
Cantor's dust is what you are left with if you start with a line, remove the middle third of that, the middle third of each one left, and so on. The lowest notes of the fractal play out Cantor's dust. You have to suppose that each note that you hear is divided yet further into smaller notes. Cantor's dust has the paradoxical property of having no total length, yet having as many points in it as the complete line (see the Maths Encyclopedia article for details).
The higher notes show the result of doing another Cantor's dust construction on each of the middle thirds that was removed at every stage, then another one on each one of those, and so on. Eventually, every point in the line is reached by this method, so it's a way of filling the line by repeating the Cantor's dust construction infinitely often.
This is what it sounds like played on a marimba, with the notes quite fast:
Cantor's dust - Geometric series scale
There would need to be many more notes between each of the ones played, indeed, infinitely many.
Notice the self similarity of the rhythmic patterns. Try listening to one of the pitches of notes only. Can you hear that each of each pair of the lowest notes is in fact double, so making a double double. They are too close together to see as separate notes in the picture.