Fractal Tune Smithy home page
![]() How the program turns your numbers into a tune
How the program turns your numbers into a tune
![]() Scales of interest to musicians
Scales of interest to musicians
(from help for Fractal Tune Smithy - download page )
Some basic concepts - The_circle_of_fifths - Using ratios to describe a scale - Equal tone systems - Harmonics and just temperament
This section is included since some users of FTS may be completely new to the subject of musical intervals. Hopefully it will give enough information so that the rest of this page will make some sense!
A tune has two components, pitch and rhythm. Scales are used to describe how the pitch varies, i.e the way the tune goes up and down in pitch.
A scale is relative. A singer can sing a major scale starting on any note. If you sing a familiar tune, then you can sing it starting from any note, and it will sound like the same tune.
When you hear music described as being in a particular key, this refers to the note the scale starts from. So for instance a C major scale starts at C.
Suppose you sing a C major scale, up as far as a G. Then decide to sing a new major scale starting from the G. Then your new key would be G major.
The idea of a key is also relative - if you sing music that starts in C major, then moves to G major, it doesn't matter what exact pitch you used for your C, so long as the two keys are related to each other in the same way. In fact a few centuries ago the standard pitch for C was much flatter, indeed, it was what we now call a B. Historically authentic performances of Baroque and early music often use lower pitches for all the keys.
Some musicians have absolute pitch, which means that if you sing a note, they can hear whether it is a concert pitch C, or higher in pitch, or lower. But this is fairly rare. Musicians with absolute pitch still hear the notes in a tune or chord as relating to each other in musical intervals, as well as hearing the absolute pitch of the notes.
When one note is double the frequency of another, it sounds like the same note, only higher. It is said to be an octave higher. Perception of notes an octave apart as the same note is universal to all cultures.
An octave can be divided into any number of equal parts as a way of fitting the pitches of scales into a system. One particularly prevalent system in use today has twelve equally spaced notes, so that each one is exactly a twelth of an octave. These twelve notes are then further divided into 100 subdivisions called cents. Any musical interval can then be expressed in cents. One can show subdivisions of a cent using a decimal point.
The major scale has two steps, large ones called tones, and small ones called semitones. Tones and semitones are not fixed in size; there are a number of ways of playing them. However in the system that uses twelve equally spaced notes to an octave, there are exactly twelve semitones to an octave. So a cent is a hundredth of a semitone in this system.
Though scales can be described using numbers, and the subject can get quite mathematical, the primary motivation is to make notes that sound good together. If it sounds good, it is okay as a scale, and that is all there is to it really.
I hope that is enough information to get you up to speed.
In some unaccompanied ethnic / folk music one might just keep to the notes of a simple scale, perhaps of a few notes only. But in other types of music, one might wish to modulate. What that usually amounts to is that one wants to be able to start a new scale to the same pattern, starting from any note of the scale one is playing in.
The interval of a fifth is the next simplest one after the octave, so if one wishes to modulate, one is likely to want to be able to go up by a pure fifth from any note reached so far.
An interval is pure if you can play both of its notes together without beats.
For instance, it's possible to play a C and a G, the first and fifth notes of the C major scale, to sound perfectly in tune. This happens when the frequency of the G is exactly one and a half times the frequency of the C. (For more on this, see Harmonics and just temperament ).
This interval is called a fifth because it is played using the first and fifth notes of the C major scale.
You can go through all the notes of the twelve tone scale by going upwards a fifth at a time, in the sequence C G D A E B F# C# G# D# A# F C.
Since the frequency multiplies by one and a half each time, the frequency of the last C is the same as for the first one multiplied by 1.5 taken to the twelfth power. This works out at close to 129.75 times the original.
That is a little over seven octaves, since seven octaves would be exactly 128 times the original frequency.
So we end up with two different C's. What is a piano tuner to do, if he or she has to tune all the C's on the piano to be in tune with each other, and all the fifths as well?
Here is the circle of fifths as a midi file:
|
Some MIDI players (noteably, old versions of Windows MPlayer) will need
a
reset
to get back to ordinary twelve tone equal temperament.
Play: B flat then c . Now play Two notes . Do you hear the same note (middle c) twice? If so your player is okay. If you hear two pitches, you can upgrade your player to one with automatic resets Windows Media Player (it's free) :) Alternatively, play Reset after listening to the clips. More details. |
Notice how the last C in the sequence is out of tune with the first one.
The answer is that it can't be done. Some compromise is needed.
One can keep pure fifths between most of the notes, but leave one wolf fifth which is out of tune. The result is a tuning which sounds good in some keys, but not in others. A tuning with all except one of the fifths completely pure is called a Pythagorean tuning.
(Original has some Tune Smithy files at this point which one can use to explore the circle of fifths in the various tunings and temperaments)
One might prefer to make all the fifths the same, and all a little bit flat. That is the equal temperament, which is the one piano tuners usually use nowadays.
It's advantage is that you can play in any of the keys, and they all sound the same.
Then there are systems in which the fifths vary in size, between pure, and somewhat flat, distributing the flatness of the wolf fifth over several keys, and these are known as well tempered scales.
Bach wrote his Well Tempered Clavier with pieces in all the major and minor keys in a well tempered scale. Confusingly, well temperament was called equal temperament in his time, because you could play equally well in all keys. See An introduction to historical tunings by Kyle Gann .
Another partial solution is to just keep going, and add a new C which is sharper than the one that began the scale. The Arabic Pythagorean scale does just that. and is constructed by continuing the circle for another five notes, and adding them in as new notes. You can modulate a fair amount with some of the modes using only notes of the scale.
You can make the Arabic Pythagorean scale from the pure fifth. What you do is go up by fifths for seventeen notes, then reduce all the notes found into the first octave by dividing them by multiples of two. The Arabic Pythagorean scale then starts at the second note of this new scale.
To make the twelve tone Pythagorean, use the same procedure, but choose twelve notes, and start at the second last note of the new scale.
In all these systems so far, the major thirds tend to be sharp - the major chords and arpeggios sound very bright.
There are other systems in which many of the major thirds are pure, and fifths are flatter even than for equal temperament.
The need for a tuning system for the notes mainly applies to keyboard instruments, and fretted instruments. Singers, and players of other instruments naturally adjust intervals they play depending on the context, so that they fit in with the harmony of the piece, and can use pure intervals in that way whenever they wish, varying the pitches of notes depending on the context of the scale or chord in which they occur.
In Pythagorean temperament, each fifth multiplies by 3/2, so after a few fifths you can get rather large numbers like 243/128. The numbers are all powers of three or powers of two. The major third is 81/64, which is rather sharp, but okay to modern ears, and the minor third is 32/27.
The just temperament scale favours simpler ratios like 15/8. The major third is 5/4 and the minor third in this system is 6/5. The major third in this system, when in isolation, can sound flat to modern ears, because we are so used to the equal temperament, in which it is rather sharp. It is however beautifully in tune once one gets used to it. It gives particularly sonorous major chords.
The term just temperament is also used more generally for systems favouring small ratios, or for ratios in general, in preference to equal or well or mean-tone temperament.
In the quarter-comma mean-tone temperament, the fifths are flatter even than for the equal temperament scale, in order to make the major thirds in tune. In this system, the wolf fifth is sharp rather than flat. It dates back to a time when musicians were used to the just temperament major third, and the wolf fifth seemed a small price to pay to be able to have pure thirds. There are other mean-tone temperaments such as sixth-comma, between quarter-comma and equal temperament.
See wolf fifth
We have already seen two ratios for the major third - 5/4 for the just temperament one, and 81/64 for the Pythagorean one.
Here they are as midi files just_then_pyth_then_just_major_thirds.mid , just_then_pyth_then_just_major_chords.mid .
When you get to smaller intervals like a tone or a semitone, many different numbers are put forward as suitable ratios for the pure interval by theorists.
The reason for all this variety in the choice of ratios is that you can get to the same note of the twelve-tone scale by various paths. For instance, you may be able to use minor or major thirds as well as fifths. It takes four minor thirds (diminished seventh), three major thirds (tritone) to get to the note an octave above. For these to reach a pure octave, the minor thirds have to be flat by about 16 cents, and the major thirds sharp by about 14 cents. The fifths for the circle of fifths have to be flat by about 2 cents.
You can also get to the octave by using six major whole tones (each needs to be flat by about 3 cents).
Here are some example midi files:
pure_circle_of_major_thirds.mid , pure_circle_of_minor_thirds.mid , pure_circle_of_bluesy_minor_thirds.mid , pure_circle_of_major_whole_tones.mid .
The ratios in the Pythagorean systems are all exprssible as multiples of two or three. For instance, 9/8 is (3×3)/(2×2×2), and 81/64 is (9×9)/(8v8) or (3×3×3×3)/(2×2×2×2×2×2). It is called a three limit scale, because it only goes up to 3.
In the just temperament scale, the ratios are all multiples of two, three or five. The reason is that they are all constructed using fifths and major thirds, which use the ratios 3/2 and 5/4, and these intervals can only introduce extra multiples of three or five, (and of two to shift notes into the same octave)
See Harmonics and just temperament .
For the bluesy minor thirds, you need the ratio 7/6, so this needs a seven limit scale.
Scales have been developed with ratios involving numbers such as 7 or higher. I have included one of these from an article by David Canright as the 7-limit twelve-tone scale in the Scales box. It includes the blues notes 7/4 and 7/6.
You can also find his 13 limit scale from Scales box | More Scales | Canright's 12-tone scales from On Piano retuning.
You can try out all these scales with the program, and play in them using the p.c. keyboard, using the New Scale... window. To start with, you may want to choose a temperament authentic for the voice. The choir voices are good for the just temperament, as choirs tend to sing pure thirds to bring out the sonority of chords.
The harpsichord is suitable for the mean-tone temperament. The trumpet is good for the harmonic series, as those are the notes played on a natrual trumpet. The Pythagorean temperament sounds well on stringed instruments, as they tune their open strings in perfect fifths, though in actual practice, string players play other intervals in various ways depending on context. The well-tempered scales are suitable for an organ. The Koto and Shakuhachi are good for the Japanese Koto scale. The Slendro and Pelog scales can be played with chromatic percussion, strings, flute, and ensemble.
Have a look in the Groves Dictionary of music if you want to see lots of details about all this. For instance, the entries on INTERVAL, JUST TEMPERAMENT, MEAN TEMPERAMENT, and PYTHAGOREAN TUNING.
For an on-line source, see Just intonation explained by Kyle Gann .
Also look at the articles on just intonation on the web by David Canright . The ones especially relevant here are: A Tour Up The Harmonic Series , On Piano Retuning , Pentatonics I Have Known , and Superparticular Pentatonics .
I used his articles as the source for the 7-limit twelve-tone scale, and for some scales used in the example compositions with the program. He has many more, including some new ones made, or found in computer searches.
The Intervals box lets you describe scales using ratios, decimals, or formulae.
You can use pure ratios, and the cents notation (a cent is a hundredth of a semi-tone).
The ratios you most often encounter in scales are closely linked to the harmonic series, see Harmonics and just temperament .
It is conventional to show the 1 as 1/1 and the octave as 2/1 (Tune Smithy shows them as 1, and 2, to save space in the box, but you can use the conventional notation by ticking File | Number Options | Whole number ratios as 1/1, 2/1, ... )
Here are some scales in cents, ratios, or mixed notation. They are all on the Scales drop down list.
Werckmeister III scale (1681): (famous historical well tempered scale from the time of Bach)
1/1 256/243 192.180 cents 32/27 390.225 cents 4/3 1024/729 696.090 cents 128/81 888.270 cents 16/9 1092.180 cents 2/1
Vallotti & Young scale (Vallotti version) (famous historical well tempered scale from Mozart's time)
1/1 94.135 cents 196.090 cents 298.045 cents 392.180 cents 501.955 cents 592.180 cents 698.045 cents 796.090 cents 894.135 cents 1000.000 cents 1090.225 cents 2/1
Pygmie scale:
1/1 8/7 21/16 3/2 7/4 2/1
Gender wayang from Pliatan, South Bali (Slendro), 1/1=305.5 Hz
1/1 235.419 cents 453.560 cents 704.786 cents 927.453 cents 2/1
Modern Pelog designed by Dan Schmidt and used by Berkeley Gamelan
1/1 11/10 6/5 7/5 3/2 8/5 9/5 2/1
Gamelan Saih pitu from Ksatria, Den Pasar (South Bali). 1/1=312.5 Hz (this is the Pelog scale used on the program's drop down list)
1/1 153 cents 315 cents 552 cents 706 cents 848 cents 1058 cents 2/1
A folk scale from Rajasthan, India
1/1 9/8 5/4 4/3 3/2 15/8 2/1
Japanese pentatonic koto scale
1/1 9/8 6/5 3/2 8/5 2/1
Xylophone from West Africa
1/1 152 cents 287 cents 533 cents 724 cents 890 cents 1039 cents 2/1
Arabic 17-tone Pythagorean mode, Safi al-Din :
1/1 256/243 65536/59049 9/8 32/27 8192/6561 81/64 4/3 1024/729 262144/177147 3/2 128/81 32768/19683 27/16 16/9 4096/2187 1048576/531441 2/1
If you tick As steps above the Intervals box, you can see the intervals as the ratios from the previous note.
For instance, the Arabic 17-tone scale, if you choose to show the ratio from the previous note, turns out to be made up of intervals of two sizes, 256/243, and 531441/524288, which you can compare with the Pythagorean diatonic with ratios 9/8 and 256/243. The ratios shown in red are in the Pythagorean 12-tone scale (all of them are there except for 729/512 and 243/128). The widest intervals of this Arabic scale are the same size as the smallest ones of the Pythagorean diatonic one, and two wides plus one small are the same size as the wide notes of the Pythagorean diatonic. The intervals are in the order W, W, S, W, W, S, W, W, W, S, W, W, S, W, W, W, S (W for wide, S for small), comparing with W, W, S, W, W, W, S for the Pythagorean diatonic.
Bohlen Pierce scale
1/1 27/25 25/21 9/7 7/5 75/49 5/3 9/5 49/25 15/7 7/3 63/25 25/9 3/1
This one is rather unusual as it repeats at an octave plus a fifth, instead of at the octave.
You can find many more in the scales archive for the freeware SCALA program by Manuel Op de Coul.
For details about the Bohlen Pierce scale:
Since twelve is divisible by two, three, four and six, musicians can play other equal divisions of the octave using notes from the twelve tone scale.
The diminished seventh chord, such as C D# F# A C has four equal divisions of a minor third, and is much used in Western music
The tritone with three equal divisions C E G# C, and the whole tone scale, with six equal divisions of a whole tone, such as C D E F# G# A# C are also used. The one with two equal divisions, is C F# C.
The Javanese Slendro scales have five approximately equal divisions in each octave.
They don't correspond to anything in Western music, and have their own unique flavour which has fascinated Western composers, Debussy being an early example. The Pelog scale is an unequal seven tone one. The originals of these scales are also rather unusual because they often have detuned octaves - getting flatter with increasing pitch. Try this one: Gamelan kodok ngorek (1/1=270 Hz)
1/1 227.965 cents 449.275 cents 697.675 cents 952.259 cents 1196.79 cents
To listen to original Balinese and Javanese music Bali and Beyond , and for an overview of the gamelan, Gamelan virtual tour (Chico's music heritage network) .
Thai music uses a system of seven roughly equally spaced notes, and three modes for this system are also included with the program.
Music theorists have also introduced scales of 19 and 31 notes among others. See MICROTONAL in Groves. The reason for these particular numbers is that they give a way to divide the octave in equal spacings that preserves many almost pure intervals.
The diatonic scale for the 31 note system is
notes 0 5 10 13 18 23 28 31 (for the octave)
or in degrees 1 6 11 14 19 24 29 32
For the 19-tone system, it's
notes 0 3 6 8 11 14 17 19
or in degrees 1 4 7 9 12 15 18 20
For tables showing closeness of match to the pure just temperament intervals:
See Microtonal scales (Microtonal synthesis home page)
Play a low note on a stringed instrument. Then lightly touch the middle of the string with one hand while continuing to bow (or pluck) with the other, and you will get the note an octave above. Touch a third of the way across, and you get the note an octave and a fifth above. A quarter of the way across, and you get to two octaves.
In the next octave you get the major third, fifth again, and then the seventh harmonic is a note which isn't used in our system, so sounds out of tune to us (ratio 7/4). It is used in jazz. Then you get another octave again, this time three octaves above.
The notes get gradually closer together as you get higher.
harmonic_series_first_five_octaves.mid
|
Some MIDI players (noteably, old versions of Windows MPlayer) will need
a
reset
to get back to ordinary twelve tone equal temperament.
Play: B flat then c . Now play Two notes . Do you hear the same note (middle c) twice? If so your player is okay. If you hear two pitches, you can upgrade your player to one with automatic resets Windows Media Player (it's free) :) Alternatively, play Reset after listening to the clips. More details. |
Here they are on a conventional score.
This time on a special score which lets you position notes accurately according to pitch (the dashed lines are all Ds)
In fact, all these notes are present in the original low note, and if you have keen hearing, you might be able to hear some of them, as its "overtones". All you are doing by touching the string lightly is to select out some of the overtones by damping other ones so that they stop sounding. (Some instruments, notably the piano, and the church bell, have extra non harmonic partials, which are out of tune with the fundamental and contribute to the characteristic piano, and bell sounds).
If you are a string player yourself, try sounding an overtone, then play the original note, and see if you can hear the overtone still sounding.
Since all the overtones belong to the same note, they sound good together. More details .
It can sometimes be confusing that ordinals such as "fifth" are used in two ways in this subject.
Fifth, used on its own, refers to the fifth note of the major scale. In this case, the fifth note you reach if you sing a major scale upwards from the note that starts the harmonic series.
When one wishes to talk about harmonics, one says third harmonic, fifth harmonic, ....
The other thing one has to get used to is that notes that are an octave apart sound as if they are the "same note", only higher. So the third, sixth and twelfth harmonics are all the "same note"; they are all fifths. They are the octave and a fifth, two octaves and a fifth, and three octaves and a fifth above the first harmonic, and those notes are all the fifth note of the major scale in their respective octaves.
The fifth note is the same in both minor and major scales, but the third differs, so one also talks about the major or minor third. If one says "third" on its own, this is understood to be the major third unless the context is clearly about minor thirds.
To add to the potential for confusion, by coincidence, the fifth harmonic is the third note of the major scale, and the third harmonic is the fifth note of the major scale. Hopefully that is understandable now.
A pure major chord, as it is most usually described, is
1/1 5/4 3/2 2/1
Here 3/2 is the third harmonic, originally in the second octave, and divided by two to bring it down into range. The 5/4 is the fifth harmonic, in the third octave. It's divided by four this time, because you have to drop it down by two octaves to get the note back into the same octave as the 1/1, 3/2 and 2/1.
If you multiply a ratio by two, or divide it by two, you get the "same note".
Starting from C, the notes of the harmonic series are:
C C G C E G - C D E - G - - B C 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
The ones shown with dashes are out of tune in the ordinary twelve-tone scales.
in_tune_harmonic_series.mid (played on 'cello)
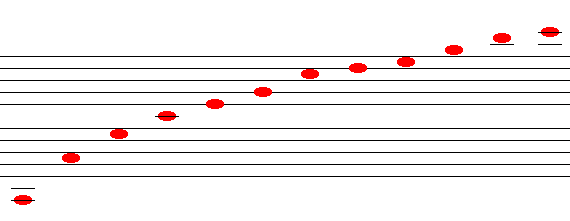
We've already got all the white notes except for F and A.
Here it is again, this time showing only the new notes each time, all transposed down into the same octave (and ending with the octave as an extra note). The original harmonic series notes are shown in brackets.
in_tune_harmonic_series_new_notes.mid (harmonic series: 1 3 5 9 15 2).
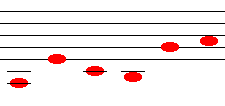 (base clef)
(base clef)
In sol fah, the notes are doh, soh, mi, re, ti (then doh' to end it)
Here it is with all the notes. Tune drops back to the fundamental after each of the "out of tune" notes. They aren't really out of tune; notes of the harmonic series always sound good together, but they are certainly more adventurous.
all_harmonic_series_new_notes.mid (harmonic series: 1 3 5 7 1 9 11 1 13 1 15 2).

(sharps in blue)
The adventurous notes are 7/4, 11/8, and 13/8.
We can now express all the new notes as ratios. For instance, the B is 15 times the fundamental. You need to drop it down a few octaves to get it into the same octave as the fundamental, which you do by dividing by two as many times as needed. The result is 15/8.
The other notes are D = 9/8, E = 10/8 (= 5/4), and G = 3/2.
Here are the notes of the scale so far in ascending order:
1/1 9/8 5/4 3/2 15/8 2/1
As a tune smithy file
diatonic_notes_from_harmonic_series.mid (played on violin this time).
We can find the missing F because it's a fifth below C, and the A because it's a third above the F (alternatively, as a fifth below E).
Using 3/2 for the fifth, and 5/4 for the major third, the F is 2/3, or moving it up by an octave, 4/3. The A is then a third above that, so it's ratio is 4/3 times 5/4, which is 5/3.
As a tune smithy file
diatonic_notes_from_harmonic_series_with_F_and_A.mid
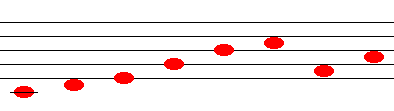
(treble clef)
So the complete just temperament diatonic (i.e. major) scale, after adding in 4/3 and 5/3, is
1 9/8 5/4 4/3 3/2 5/3 15/8 2
We can now fill in the black notes using major thirds. We have to multiply by 5/4 to go up by a major third, and divide by it, or equivalently, multiply by 4/5, to go down a major third.
Going down a major third from the octave C gives 2 times (4/5), so 8/5, which is our A flat / G sharp. Doing the same from the G at 3/2 gives 3/2 times 4/5, which is 6/5, our E flat / D sharp. We can go down from F at 4/3 to get D flat / C sharp as 16/15. Going down a major third from the D at 9/8 gives the B flat / A sharp as 9/10, or after moving it up an octave into range, 9/5.
Notice, that if you went up a major third from E, you would get to G sharp as 5/4 times 5/4, or 25/16 instead of 8/5, which is how a musician sensitive to just intonation major thirds might play it in the scale of E major from this E.
If playing in pure just intonation, you could be forced to play a minute shift in pitch when changing from a G sharp to an A flat.

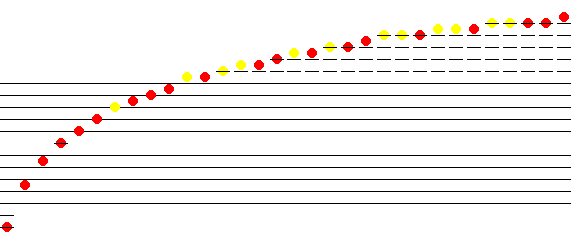
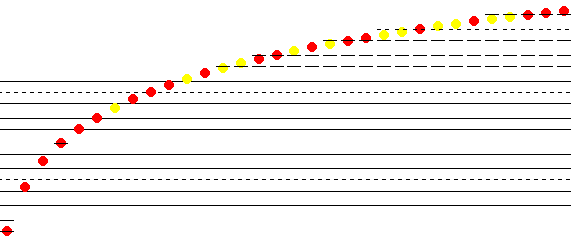
These are the notes on a conventional score with flats in yellow, sharps in blue
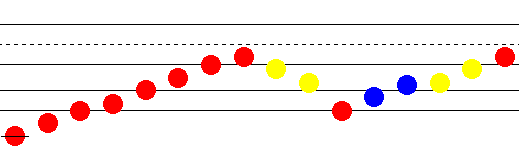
The same notes, but this time positioned exactly, by pitch, so that you can see that the G sharp (highest of the two blue notes) is a little flatter than the A flat (lowest of the two yellow notes).
This is what one sounds like: enharmonic_shift_for_G_sharp.mid (plays major scale in C, then goes down to the A flat in A flat major, then goes up to the G sharp in E major from the E of the just intonation C major scale, then shifts back to the first tuning for the A flat ready to go back up to the original C in A flat major).
We now have all the notes except the F sharp (or G flat). It's a major third above D at 9/8, so 9/8 times 5/4, which gives 45/32, the most complicated ratio in the just temperament twelve tone scale.
Try just_temperament_twelve_tone_constructed_from_diatonic_scale.mid
The notes played are
1/1 9/8 5/4 4/3 3/2 5/3 15/8 2 8/5 3/2 6/5 4/3 16/15 9/8 9/10 9/8 45/32 1/1 (sharps in blue, flats in yellow).
So the complete twelve tone scale is
C C# D D# E F F# G G# A A# B C 1 16/15 9/8 6/5 5/4 4/3 45/32 3/2 8/5 5/3 9/5 15/8 2
This scale is great for music with lots of major thirds and that doesn't stray too far from the basic key.