#  5.  3. ../manuelopdecoul/efg-e Show tree

What is an Euler-Fokker genus?

In ancient times the Greeks made a distinction between different genera. The fourth was the interval between the two extreme tones of the tetrachord. Two other tones divided this distance into three intervals, in various different ways. This multiformity gave rise to a system of classification into genera: the enharmonic, the chromatic and the diatonic genus.
The Euler-Fokker genera (plural of genus) are a different kind of genera, but it's the same sense of the word. In the Western music of today, not the fourth but the octave is the basic interval of tone relations. Therefore all tones are shifted as many octaves as necessary to bring them within the range of one octave. The relations between the intervals themselves form the distinguishing characteristic of the genus. An Euler-Fokker genus originates when one repeatedly adds certain pure intervals to a fundamental tone to form a network of tones. The pure intervals that are applied are the basic intervals of our tone system: the pure fifth (frequency ratio 2:3, therefore symbolised by the number '3'), the major third (frequency ratio 4:5, or '5') and the harmonic seventh (4:7 or '7', clearly smaller than the normal minor seventh and thus absent in the common 12-tone system). The construction of an Euler-Fokker genus is indicated by means of a kind of formula, for instance [33377] {D+,G-}. D+ (a small step higher than D) is the fundamental of the network. The genus is formed by adding three fifths and two harmonic sevenths. G- (a small step lower than G) is diametrically opposite to D+ and is being called the guide tone. The formula leads to the following network of tones, in which the horizontal connections represent fifths, and the vertical connections harmonic sevenths:

    Bb-  3    F-   3    C-   3    G-
    7         7         7         7
    C    3    G    3    D    3    A
    7         7         7         7
    D+   3    A+   3    E+   3    B+
[55777] {C,C#} can be sketched as follows: 

    F    5    A    5    C#
    7         7         7
    G+   5    B+   5    D#+
    7         7         7
    Bb-  5    D-   5    F+
    7         7         7
    C    5    E    5    G#
In this network the horizontal connections represent major thirds, and the vertical ones harmonic sevenths. After stacking the intervals, the tones are transposed down as many octaves as necessary to bring them inside the range of one octave. One can choose the name of the fundamental at will, like D+ in the first example. These genera have been employed by Alan Ridout. We can clarify this first example by giving the frequency ratios:
 
  0:         1/1          C          0.000 cents
  1:         9/8          D        203.910 cents
  2:         8/7          D+       231.174 cents
  3:         9/7          E+       435.084 cents
  4:        21/16         F-       470.781 cents
  5:       189/128        G-       674.691 cents
  6:         3/2          G        701.955 cents
  7:        27/16         A        905.865 cents 
  8:        12/7          A+       933.129 cents
  9:         7/4          Bb-      968.826 cents
 10:        27/14         B+      1137.039 cents
 11:        63/32         C-      1172.736 cents 
 12:         2/1          C       1200.000 cents

The number of intervals which form the basis of an Euler-Fokker genus is called the degree. The genera [33377] and [55777] are genera of the fifth degree. Genera of a particular degree do not all have to have the same number of tones. The number of tones also depends on the exponents of the basic intervals. ([33355] can also be notated as [3³.5²].) The degree is thus the sum of the exponents. One obtains the number of tones by increasing all exponents with one and taking the product of that. So [3³.5²] has (3+1)×(2+1) = 12 tones. It's written sometimes also as [2m.3³.5²] to indicate the arbitrariness of the number of octaves, as in the following figure:

Spectra of genera
Fig.1: Spectra of the genera of the third degree, illustration from Rekenkundige bespiegeling der muziek.

Each line herein depicts one tone of the frequency spectrum. The regular and sometimes irregular character of the genera becomes visible this way. They are of the third degree, so with three, not necessarily different, generating factors. The tone lattice of the first three is 1-dimensional (they contain one factor), the next ones 2-dimensional and only the last one is 3-dimensional because of the three different generating intervals 3, 5 and 7 - ignoring the octave with factor 2.
Euler considered in his Examination of a new music theory (1739) only genera (named genus musicum) with generating factors 3 and 5. Fokker added the factor 7 to them and made an inventory of the different genera (1942-1946, 1966). Euler had already noted the possibility of a factor 7 however, but left it at that. One doesn't have to leave it with these three factors, a genus can be made with an arbitrary combination of two or more prime factors.

An Euler-Fokker genus can also be defined as a complete contracted chord. This term is Fokker's. The term complete chord is coming from Euler. A complete chord has a fundamental and a guide tone, with in between all tones that are both a whole multiple of the fundamental, and a divisor of the guide tone. The guide tone is also a whole multiple of the fundamental. For example if we take the number 1 for the fundamental, and the number 12 for the guide tone, then the complete chord consists of the tones 1, 2, 3, 4, 6 and 12. We can also reverse this and say that no tones can be added to a complete chord without altering the ratio of the fundamental to the guide tone. This quotient of guide tone and fundamental is called the tension number or exponens (by Euler: Exponens consonantiae). Let's take as another example the following complete chord: 1:3:5:15. This is the genus [35] {C,B} of the second degree. Bringing these tones within the range of one octave, they become 1/1, 3/2, 5/4 and 15/8 (C, G, E and B), and this is then a complete contracted chord. The 1/1 (C) now becomes the substitute fundamental, and 15/8 (B) is called the substitute guide tone of the complete contracted chord, identical to the fundamental and guide tone of the Euler-Fokker genus. The shape of the tone lattice of an Euler-Fokker genus or a complete chord is always a rectangle, or a rectangular parallelopiped in the 3-dimensional case.
The mathematical definition of the fundamental is the greatest common denominator of the tone frequencies. The guide tone is the lowest common multiple of them.

The genera of the third degree are preprogrammed among others on the 12-tone manual of the Fokker-organ. Although the Euler-Fokker genera are strictly speaking tuned pure (just), they can also be played in the 31-tone equal tempered system because the three basic intervals are well approximated in it. The beatings caused by the slight impurity make the sound of them more lively. The major third in 31-tone equal temperament is formed by 10 steps, the fifth by 18 steps and the harmonic seventh by 25 steps.
With the above notation of + (1 step higher) and - (one step lower), a step of 1/31 octave or a fifth tone is meant. In Fokker's notation system this is indicated with the 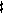and 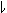signs respectively. Bb- (3 steps lower than B) is B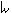 en C#+ is C.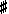
There are 10 genera of the third degree:
[333] {C,A}C - D - G - A
[335] {F,B}F - G - A - B - C - E
[355] {A,B}A - B - C - E - E - G
[357] {C,A}C - D - E - F - G - A - B - B
[377] {C,D}C - D - F - G - G - B
[555] {C,B}C - E - G - B
[557] {A,D}A - B - C - D - E - G
[337] {C,C}C - D - F - G - B - C
[577] {C,B}C - D - E - G - B - B
[777] {C,F}C - F - G - B
The book Adriaan Daniël Fokker - Selected musical compositions (1948-1972), with introduction by Rudolf Rasch, Corpus Microtonale vol. 1, Diapason Press, Utrecht, 1987, has an extensive overview of the genera with the compositions written in them.

See also the article Expériences musicales avec les genres musicaux de Leonhard Euler contenant la septième harmonique, which contains some scores of compositions of Adriaan Fokker and Jan van Dijk.
Go to the music page to listen to these compositions via MIDI-files.

Euler and music is an article by Patrice Bailhache that also goes into the genera. The original French version is called La musique traduite en mathématiques: Leonhard Euler.

With the computer program Scala it's possible to calculate Euler-Fokker genera with arbitrary factors and of any degree and analyse them.

Manuel Op de Coul, 2000

Startpagina | Home page