|
|
Seeds etc | User guide | Main Window | Musical note intervals | Scales | Midi in | Analyse sound |
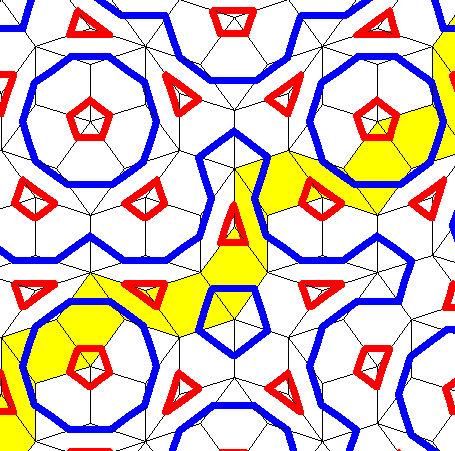
Picture shows the Penrose tiling.
This pattern never repeats exactly. Patches of it do repeat - such as the five-fold star within a decagon that you can see three copies of in this region, but the whole pattern never does.
The preset two beat rhythm plays long and short beats corresponding to the wide and narrow rhombs along a row of a Penrose tiling, such as the row highlighted in yellow.
The one shown would be played as L S L L S L L S L S L L S L (starting from bottom left).
The idea of this page gives some connections of the Fibonacci rhythms with other areas of mathematics and physics, which may interest some users of FTS of a mathematical or scientific inclination.
You may know of the way of drawing a stack of cubes using hexagons, each divided into three rhombs.
The Penrose tiling shows a stack of five dimensional hypercubes cut through at a particular angle.
Here is a page with a link to a fun applet for making your own non periodic tilings interactively.
http://www.geom.umn.edu/apps/quasitiler/about.html
Choose five dimensions for the Penrose tilings, and related tilings.
One especially interesting thing about the penrose tilings is that they have arbitrary large areas of five fold symmetry, and one can show that the only possible symmetries of a periodic tiling are 2, 3, 4, and 6. (and 1 = no rotational symmetry).
Some special crystals have been grown in the last couple of decades or so with strikingly symmetric five fold diffraction patterns
See this page:
http://www.cmp.caltech.edu/~lifshitz/quasicrystals.html
These diffraction patterns caused great surprise to crystallographers when first seen - nothing like that had been expected. They tried all sorts of alternative explanations, but now it is generally accepted that they are related to non periodic tilings, some of the crystals correspond to the Penrose tilings, some to other 2d non periodic tilings, and some to 3D versions of the Penrose tilings. They are known as Quasicrystals (they don't fit previous definitions of a crystal as they never repeat, even though they are highly ordered).
Quasicrystals may not need to be built up using two units as there is a version of the penrose tiling that consists of a single decagonal patch, which you fit together with rules about how adjacent patches overlap. They could form using similar decagonal units with adjacent units sharing atoms. Details of how Quasicrystals can form at an atomic level remains somewhat mysterious, and a very active area of research at present.
They are produced by rapidly cooling a metal alloy of some particular composition at a precisely controlled rate. Depending how you do it, you get periodic tilings, periodic approximations to Penrose like tilings with larger and larger patches of tiles for the repeat, then the non periodic Penrose tiling itself (or something that very closely resembles it anyway).
The Fibonacci sequence can be made in an alternative way using a cut through squares at a particular angle.
Scroll down to the fig: Example for a 1D-quasiperiodic sequence (Fibonacci chain) on this web page: Quasicrystals
The best book for an introduction to the whole area is the one by Grunbaum and Shepherd, "Tilings and patterns", 1986 (so doesn't include the more recent material). Includes the Penrose tilings. Highly mathematical, pitched for maths undergraduates or post-graduates, but has lots of pictures of the tilings, so you can just skip the more mathematical sections. You need the unabridged version - there is a student edition that leaves out the non-periodic tilings material. Non mathematicians seem to find it of value.
How to prove that the Penrose tiling is non periodic
This is an explanation of the idea behind the method in ordinary language, rather than the actual proof. You can find the proof itself in Grunbaum and Shepherd (unabridged edition).
Basic idea is that you make a tiling by starting from a single tile, and dividing it into smaller tiles in a particular way, then repeat the process on those smaller tiles, and so on. This is called inflation.
Note, this subdivision quite often works by dividing each larger tile into a number of fragments, rather than into whole tiles. You get the whole tiles from the way the fragments from adjacent tiles fit together.
There is a theorem that states that if you can make arbitrarily large patches out of a set of tiles, then you can make an infinite tiling with them. So if a set of tiles has an inflation, it tiles out to infinity.
The reverse of this process, grouping together smaller tiles to make larger tiles, is called deflation.
Now you need to prove that one can go back again (deflation) in a unique way.
It is easy to make a tiling with a non unique deflation. In the periodic tiling by regular squares, you can group four squares together to make a larger square, so it has a deflation, but it's not a unique one. There are four ways of doing it
Start with any particular square, and the four ways are to include the square to right or left, then include either the two squares above or below. Once you've made the choice for one square, you then extend it to all the other tiles to make a tiling by squares twice the size.
The square tiling is of course periodic.
However if you can show you can only go back in a unique way, your tiling is aperiodic, by a theorem:
THEOREM: A self-similar tiling with a unique deflation has no translational symmetries
For the proof, see
http://www.math.okstate.edu/mathdept/dynamics/lecnotes/node27.html
The previous page:
http://www.math.okstate.edu/mathdept/dynamics/lecnotes/node26.html
introduces the idea of a self similar tiling.
So if you can show that a particular tiling has a deflation, and that the deflation is unique, you know that it never repeats exactly, i.e. is non periodic. You can use exactly this method to show that some of the rhythms are non periodic. See How can one tell that this rhythm will never repeat .
However the Penrose tiles have a much more remarkable property than this. The tiling shown does indeed never repeat, but more than that, no other tiling you can make with them will repeat either. A set of tiles with this property is known as an aperiodic set.
If you can show that a particular set of tiles
1. can only fit together to make tilings that have deflation.
and
2. that the deflation is unique
you can conclude that all the tilings you can make with those tiles are non periodic.
Any rhomb tiles periodically by itself.
So to make the set of penrose rhombs into an aperiodic set, you need to add matching rules to restrict the ways they can fit together. In the tiling shown, the matching rule is that the coloured lines have to run continuously from each tile to the next in the pattern.
You can alternatively replace these by jigsaw like curves added to the edges of the tiles, so they can only fit together certain ways.
When you do that, then all the tilings by the Penrose rhombs are non periodic.
Notice that establishing the inflation / deflation and uniqueness of it isn't enough. When the Penrose tiles were first popularised, some people were under the impression that this was all one needed to do to make an aperiodic set of tiles.
The most tricky part of the proof is to show that the tiles can only fit together to make tilings which can be deflated. That is done case by case, looking at all possible patches of the tiles, until you get to a large enough patch to guarantee the deflation.
The existence of non periodic sets was first proved by Wang, who did it by constructing an example set, made by varying a basic square template tile by adding matching rules to it, to make a set consising of several thousand tiles (when you count all the combinations of matching rules needed - he didn't make all these tiles individually!).
The Penrose set, at only two tiles, was a record breaker when released.
This page has lots of links:
http://www.ics.uci.edu/~eppstein/junkyard/penrose.html
The idea of coding for Fibonacci tone-scapes in FTS derives from a picture of a Penrose tiling with intervals assigned to the vertices on the last page of this entry: D'Alessandro, Like a Hurricane (XENHARMONIKON 12) from the Wilson Archives
Thanks to Manuel Op de Coul for telling me about this picture.