Icosahedron |
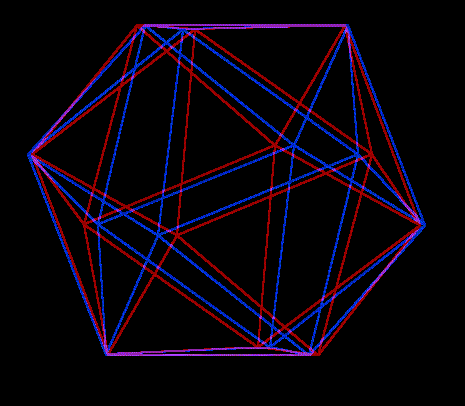 |
Made with Virtual flower
To make a geodesic sphere, start with a geometric shape which has regular triangular or square faces.
The icosahedron is often used here because it is already close to a sphere in shape.
Now divide each face into smaller triangles like this:
What you do is to add a new vertex in the middle of each of the original sides. Then by connecting those up, divide each of the original faces into four smaller triangles.
Then move the new vertices out to the surface of a sphere around the original shape.
This is probably the most commonly used small geodesic sphere
If we want a larger or more spherical shape, divide the original faces into more smaller triangles first - here we add two new vertices to each of the original sides:
We can keep going in this way as far as we like:
Though the icosahedron is the commonest choice, one can use any regular geometric shape with square or triangular faces in the same way
The triangles are uneven in size - that's because they get stretched when you move the vertices out to the sphere. Actually the icosahedron ones are strethced too and are in several different sizes / shapes - architects have to take account of that. However it is easily noticeable for the tetrahedron.
Here is an octahedron. The original faces aproximate to great circles for this figure - see the shapes with equators page.
Triangles are particularly useful for architectural design
However, for pure maths, one may as well carry out the same construction with squares too.
You will see this cube against a white background in the interactive view you get when you click on the image
It flips over to a distorted cube shape if you do it against black because it especially needs the red and blue colours to combine when the lines cross
One can also use squares and triangles in the same figure:
This is another one with great circle equators.
You can make anaglyphs like these in my Virtual flower Windows program.
Click on any of the pictures to show an interactive anaglyph which you can turn and see it from other angles - needs a VRML plug in installed such as the Cortona VRML client
The anaglyphs are ptimised for a distance to the screen of twenty times the eye separation. As you look at them from closer or further away, the figure will flatten or stretch.