| Home | Ray Traced models | Anaglyphs | Interactive models | Virtual Flowers | About me | Tunes | Jacob Van Eyck | Fractal Tune Smithy |
The rhombic dodecahedron, triacontrahedron, and golden rhombohedra
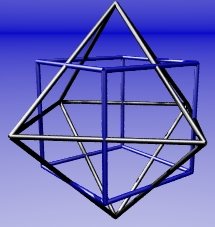
Double the height of the black octahedron in the picture on my home page, and its edges will intersect with those of the blue cube, at right angles:
Join the vertices together and you get a rhombic dodecahedron. It has twelve rhombic faces
(without the octahedron)
(with the
octahedron)
You can build it out of this rhombohedron
The diagonals of its faces are in the ratio of one to root two.
This shows how it is done.
Scale the green icosahedron of the original picture up by the square of the golden ratio, and it's edges will meet the edges of the cyan dodecahedron at right angles. The next two images show the original picture, and the green icosahedron after it has been scaled up by the square of the golden ratio.
Join the vertices of the dodecahedron to
the vertices of the icosahedron, and you get this:
(picture
leaves out the icosahedron edges)
This new shape in magenta is a triacontrahedron - it has thirty faces.
You can build it out of the two golden rhombohedra, so called because the diagonals of their rhombic faces are in the golden ratio to each other.
The one on the left is the oblate golden rhomb, which is flattened in shape, while the one on the right is prolate, which means it is elongated in shape.
These images show how you can build a rhombic triacontrahedron step by step with the two golden rhombohedra.
A golden rhombic dodecahedron,
with the ordinary rhombic dodecahedron again for comparison.
A golden rhombic icosahedron - it has
twenty exterior faces.
The rhombic
triacontrahedron built out of golden rhombohedra.
Click for a larger image with the central rhombohedron highlighted
Perhaps you can see the golden rhombic icosahedron that makes up the lower left of the triacontrahedron. And if you look closely, you will see some copies of the golden rhombic dodecahedron there as well, for instance, there is one in the front with five faces on the exterior of the triacontrahedron.
 |
 |
| The golden icosahedron on its own | . The golden dodecahedron on its own. |
More mathematical images (start of page)
More mathematical images (golden rhombohedra)