| Home | Ray Traced models | Anaglyphs | Interactive models | Virtual Flowers | About me | Tunes | Jacob Van Eyck | Fractal Tune Smithy |
[split view] [or split vertically] You can use this to keep the first picture in view while you scroll through the rest of this page. (Needs frames.) [restore to single view]
All these images were generated using Povray, an amazing freeware ray tracer: Povray home page. The idea of a ray tracer is that you define a model, the light sources that illuminate it, and the properties of the materials (shiny, metallic, matt, etc) and then it traces light rays from the light sources, via the model to the viewpoint as a way to get an image of the model using very realistic visual effects.
vertices, stella octangula, volumes, starting the process all over again, Povray
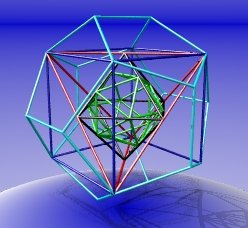
An icosahedron within an octahedron within a tetrahedron within a cube within a dodecahedron.
The vertices of the green icosahedron divide the edges of the black octahedron in the golden ratio. This ratio is a number that crops up often in mathematics, and also in other area such as growth in biology, numbers of spirals in sunflowers and pineapples, and the work of artists who think of it as beautiful.
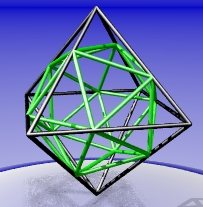
Around each octahedron vertex, the icosahedron vertices are alternately closer, and further away.
The vertices of the black octahedron meet the midpoints of the edges of the red tetrahedron.

The red tetrahedron joins alternate vertices of the blue cube to each other.
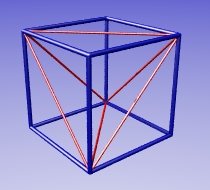
And finally, the cube joins together some of the vertices of the dodecahedron,

You can inscribe another tetrahedron in the cube
The tetrahedron, cube, octahedron, icosahedron and dodecahedron are known as the platonic solids. They are also called perfect solids, because all the faces have the same number of sides, and the faces meet together in the same way at each vertex. Here is a link to the article on Plato in the history of mathematics archive at the University of St Andrews. At the end, there is a link to the platonic solids.
This way of constructing the five platonic solids gives one way of finding all their volumes.
The rhombic dodecahedron, triacontrahedron, and golden rhombohedra.
The small stellated dodecahedron
Returning to the original picture, one can add an extra copy of the green icosahedron on the outside, its edges intersecting with the cyan dodecahedron.
Then you can start the process all over again, building another octahedron around that one, and so on. Here is the result as far as the second dodecahedron.

You can see the first dodecahedron inside, with its edges intersecting with the second icosahedron.
After four iterations you get:
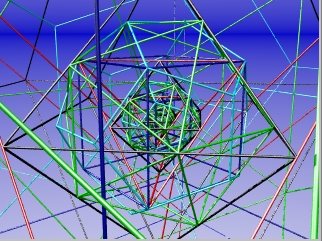
A few iterations later, and the edges are beginning to disappear into the distance on this scale of image.
Click for a much larger image (358 Kb JPEG, 1280x1024, and 10 iterations)
To down load my Povray description file which can be used to generate any of the images on this page, click here:
Persistence of vision ray tracer scene description of the main image (29 K text file)
I have some interactive models which you can move and turn around on the screen with your mouse.