| Home | Ray Traced models | Anaglyphs | Interactive models | Virtual Flowers | About me | Tunes | Jacob Van Eyck | Fractal Tune Smithy |
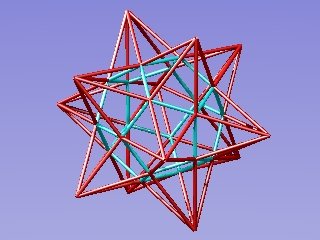
The small stellated dodecahedron

You get this by scaling the icosahedron up by a ratio of the cube of the golden ratio relative to the one in the original picture, and joining the dodecahedron vertices to the icosahedron vertices. The method is identical to the construction of the triacontrahedron, with the icosahedron scaled up once more by the golden ratio.

This shows the connection with the triacontrahedron - the small stellated dodecahedron is like a triacontrahedron, with the original icosahedron vertices moved further away from the centre
The small stellated dodecahedron has twelve intersecting pentagram faces.
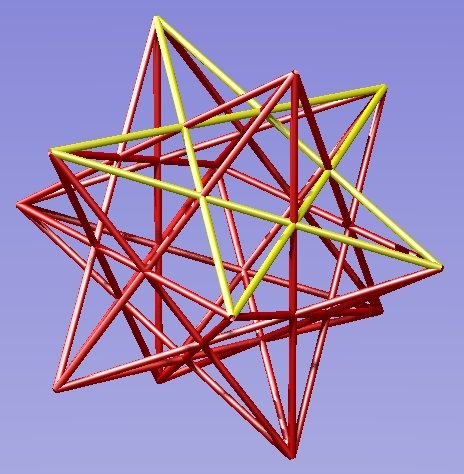
When describing these mathematical figures, one thinks of the pentagram as a face with five edges. You ignore the points where the edges intersect. When you think this way, you see that the small stellated dodecahedron has twelve identical faces, which meet together in an identical fashion around each of it's twenty vertices.
The faces intersect each other, and again, you ignore the intersections. So the small stellated dodecahedron is another perfect solid, like the platonic solids. Perfect solids which have intersecting faces, or faces with edges that intersect, or both, are known as Kepler Poinsot solids.For a complete list, see Tom Gettys models, or George Hart's site with interactive models.
.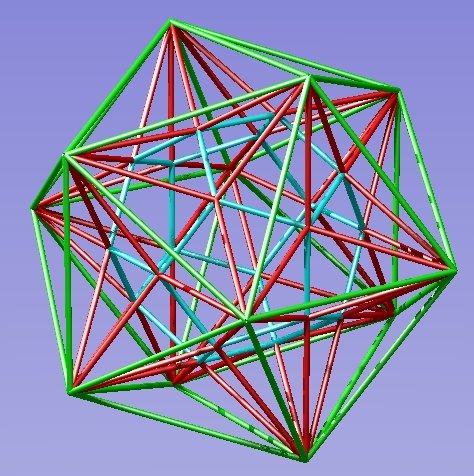
This shows the icosahedron, dodecahedron, small stellated dodecahedron, and how they all fit together.
You can make out some other shapes in the picture.
The green icosahedron edges are also the edges of twelve large intersecting pentagons. Can you see two of them parallel, and almost horizontal, above and below the centre of the picture? Together they form the great dodecahedron, which has the same number and type of faces as the dodecahedron except that it's faces intersect each other. It's another Kepler Poinsot solid.
Look at any two parallel faces of the great dodecahedron. They are joined to each other by a pattern of green triangles. Together they make a figure called a pentagonal anti-prism. An anti-prism is the same as a prism, but with the opposite faces joined together by triangles rather than by squares or rectangles. The effect is to turn each face round relative to the other, so that a vertex of one is opposite an edge of the other.
So, as you can see from the next picture, the icosahedron consists of a pentagonal antiprism with two pentagonal pyramid caps above and below.

More mathematical images (start of page)
More mathematical images (small stellated dodecahedron)