Hexany
From Wikipedia, the free encyclopedia
(see also the wikipedia entry on hexany)
Intro - Tuning - Relationship to Pascal's triangle - - Coordinates for the Pascal's Triangle of Combination Product Set
Intro
In music theory, the hexany is a six-note just intonation scale, with the notes placed on the vertices of an octahedron. The notes are arranged so that every edge of the octahedron joins together notes that make a consonant dyad, and every face joins together the notes of a consonant triad.
This makes a "musical geometry" with the geometrical form of the octahedron. It has eight just intonation triads in a scale of only six notes, and each triad has two notes in common with three of the other chords, arranged in a musically symmetrical fashion due to the symmetry of the octahedron it is based on.
This is an idea due to Erv Wilson. The Combination Product Sets are obtained as successive cross sections of an n-dimensional cube, and the numbers of vertices follow the numbers in Pascal's triangle. The Hexany is the third cross section of the four-dimensional cube.
Tuning
The four dimensions of the hypercube are usually tuned to distinct primes (sometimes to odd numbers) and a single step in each dimension corresponds to multiplying the frequency by that prime. The notes are then usually reduced to the octave (by repeated division by 2) using octave equivalence.
For example, for a 2 3 5 7 hexany, assign 2 3 5 7, to the four dimensions. Then to obtain the octahedron as a diagonal cross section of the hypercube, use all permutations of (1,1,0,0) as the coords. There for instance, (0,0,1,1) moves one step in the "5" dimension and one step in the "7" dimension and so would be tuned as 5*7.
So, to make the complete hexany, multiply the primes together in pairs to give six numbers: 2*3, 2*5, 2*7, 3*5, 3*7, and 5*7 (or 2*3*1*1, 2*1*5*1, 2*1*1*7, 1*3*5*1, 1*3*1*7 and 1*1*5*7).
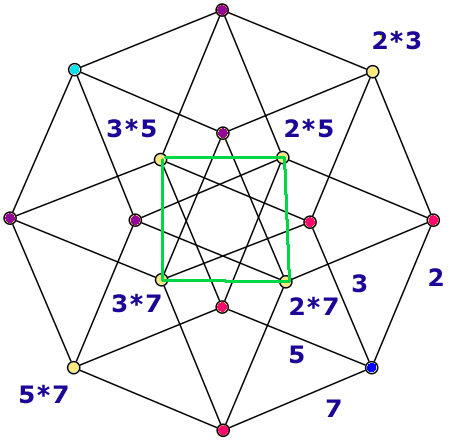
(modified from Tilman Piesk's Hypercubestar)
In this picture of a hypercube, the six hexany vertices are shown in yellow, and four of the vertices are shown connected (in green). The other two vertices join to them to make the octahedron. All the sides of the octahedron are diagonals of squares, so are the same length (root two), so it is a regular octahedron - the "squashed" appearance is because it is rotated into the fourth dimension.
Similarly the red vertices can be joined together to make a regular tetrahedron, and the purple vertices likewise. (If one finds it a bit baffling that's to be expected - a few people, like Alicia Stott, have been able to think four dimensionally but it is beyond most of us).
Then for example the face with vertices 3*5, 2*5, 5*7 is an otonal (major type) chord since it can be written as 5*(2, 3, 7), using low numbered harmonics. The 5*7, 3*7, 3*5 is a utonal (minor type) chord since it can be written as 3*5*7*(1/3, 1/5, 1/7), using low numbered subharmonics.
To make this into a conventional scale, you reduce the notes to the octave. Note that 1*1*1*1 isn't a vertex.
So the scale doesn't have a 1/1 yet. It doesn't matter which note you choose. Say 5*7. Divide all the notes by 5*7 and you get: 1/1 8/7 6/5 48/35 8/5 12/7 2/1 as your scale (up to octave reduction). For those new to this notation - the ratios notation for scales just shows the ratio of the frequencies of the notes. So for instance if the 1/1 is 500 hertz, then 6/5 is 600 Hertz, and so forth.
Relationship to Pascal's triangle
The complete row of Pascal's triangle for the hypercube in this construction runs 1 (single vertex), 4 (tetrahedron tetrad), 6 (hexany), 4 (another tetrad), 1. The idea generalises to other numbers of dimensions - for instance if you take cross sections of a five dimensional cube, you get two versions of the dekany, a ten note scale rich in tetrads, triads and dyads, which also contains many hexanies.
In six dimensions you get the twenty note eikosany which is even richer in chords. It has pentads, tetrads, riads as well as hexanies and dekanies.
In the case of the three dimensional cube, it is usual to consider the entire cube as a single eight note scale, the octany - the cross sections then are 1, 3 (triad), 3(another triad), 1 taken along any of the four main diagonals of the cube.
Coordinates for the Pascal's Triangle of Combination Product Sets
First row (square):
00
10 01
11
Second row (cube or octony):
000
100 010 001 triad (triangle)
110 101 011 triad (triangle)
111
Third row (hypercube)
0000
1000 0100 0010 0001 tetrad (tetrahedron or 3-simplex)
1100 1010 1001 0110 0101 0011 hexany (octahedron)
1110 1101 1011 0111 tetrad
1111
The octahedron there is the edge dual of the tetrahedron
Fourth row (5-dimensional cube)
00000
10000 01000 00100 00010 00001 pentad (4-simplex or pentachoron - four dimensional tetrahedron)
11000 10100 10010 10001 01100 01010 01001 00110 00101 00011 2)5 dekany (10 vertices, edge dual of the 4-simplex)
00111 01011 01101 01110 10011 10101 10110 11001 11010 11100 3)5 dekany (10 vertices)
01111 10111 11011 11101 11110 pentad
11111
The edge dual of the pentachoron for the dekany is also known as the Dispentachoron - see Convex uniform polychora based on the pentachoron (5-cell)
Fifth row (6-dimensional cube
000000
100000 010000 001000 000100 000010 000001 hexad (5-simplex or hexateron - five dimensional tetrahedron)
110000 101000 100100 100010 100001 011000 010100 010010 010001 001100 001010 001001 000110 000101 000011 2)6 pentadekany (15 vertices, edge dual of 5-simplex)
111000 110100 110010 110001 101100 101010 101001 100110 100101 100011 011100 011010 011001 010110 010101 010011 001110 001101 001011 000111 eikosany (20 vertices)
001111 010111 011011 011101 011110 100111 101011 101101 101110 110011 110101 110110 111001 111010 111100 4)6 pentadekany (15 vertices)
011111 101111 110111 111011 111101 111110 hexad
111111
References
Grady, Kraig, "Ervin Wilson's Hexany", 1/1, the Journal of the Just Intonation Network 7 (1): 8
Back to
(This page is a copy of the wikipedia page made on feb 7th 2008).
As a wikipedia article, this page is licensed under the GNU free documentation license, and I am required to include this as a condition of copying it (it was entirely my own work at the stage of this snap shot so I'm not sure if that still applies to a copy that I make of my own work, for my own web site - but in case it does).
So - here it is GFDL
To get the program, download and install Virtual Flower.


